The Black-Scholes Magic Trick, Explained!
The economist Paul Romer once compared the models used in finance with the tricks used by magicians, whose secrets are protected by the Magician’s Oath. As he wrote in 2015, “A model is like doing a card trick … Perhaps our norms will soon be like those in professional magic; it will be impolite, perhaps even an ethical breach, to reveal how someone’s trick works.” [Spoiler alert: guilty as charged.]
Of course, nothing can be kept secret forever, so once a magician has invented something like a levitation trick, as illusionists did some two centuries ago, other versions soon follow. Today, you can find explanations on YouTube, or Wikipedia. But for most audiences, the trick will still be effective.
An example of such a mathemagical trick is the Black-Scholes model, which since its publication in 1973 has served as the industry-standard model used to price financial options – those instruments which give one the right but not the obligation to buy (a call option) or sell (a put option) a stock in the future at a set price, known as the strike. The model is magically simple: in order for the price of the option to be revealed, traders only need to supply two key pieces of information: the risk-free interest rate, which can be obtained from something like a Treasury bond, and the volatility, which is an estimate of price variation (technically, it is the standard deviation of the logarithm of price changes over a period such as a year).
As financial magic shows go, the Black-Scholes model has certainly had a good run – one of the longest on Wall Street, and elsewhere – and has received rave reviews. One commentator (Ross, 1987) described option pricing as “the most successful theory not only in finance, but in all of economics.” Another (Rubinstein, 1994) said the algorithm may be “the most widely used formula, with embedded probabilities, in human history.” Even critics acknowledge the model’s importance to the field; Nassim Nicholas Taleb (1998) wrote that “Most everything that has been developed in modern finance since 1973 is but a footnote,” while in his 2008 report to shareholders Warren Buffet said it had “approached the status of holy writ” (magic being closely related to religion).
A popular component of magic shows is the prediction trick, where the magician makes a seemingly impossible prediction about an audience member or something else. The Black-Scholes formula does this but with a twist. Its trick is to present itself, not so much as a prediction, but rather as a magical machine which somehow defines the correct option price – like a mentalist who predicts the future by making it happen. And by using the machine as a calculating device, investors only seem to confirm its predictions. What kind of higher-level voodoo is this?
Such is its hypnotic hold, that it defines the very words and concepts used by quants to describe option pricing. For example there is the “implied volatility” which is the special number that must be fed into the machine in order for it to work, but whose true value can be divined only in hindsight. And then there are the “Greeks” which refer to various terms thought to describe its sensitivities, and are reminiscent of the arcane symbols employed by sorcerers. For example the symbol Δ shows how the option price depends on the current asset price, while Θ measures its dependence on time.
Even more remarkable is that the mesmerising power of the model’s spell has distracted the audience from worrying about – or often even noticing – the fact that its assumptions have no more obvious means of support than a magician’s levitating assistant.
Suspending disbelief
For example, one of its totems is that markets are “efficient” so are made up of what economist Eugene Fama (1965) called “rational profit maximizers” whose collective actions ensure that everything is priced rationally, including assets and options. If anyone still think markets are rational and efficient, then see below.
Much of the power of the model comes from its amazing use of “dynamic hedging” which assumes that someone can constantly buy and sell options and the underlying stock in such a way that the risks are always balanced. The theory appears to mathematically prove that the value of an option does not depend on the growth of the underlying asset (which is why the formula uses only the risk-free rate). And yet it obviously kind of does, which is why for something like the S&P 500 index, which tends to grow, call options (to buy) have consistently outperformed put options (to sell). This is a problem, since the test of the model is not to satisfy some abstract theorem, or even to predict what traders are paying for options; it is to predict what prices correspond to the expected payouts.
The model assumes that prices follow a “random walk”, so the probability distribution for price changes should be lognormal (i.e. the log price changes should follow a bell curve). But, it’s not. It has “fat tails” meaning that the chances of extreme price changes, such as a crash or a spike, are much higher than predicted by the model.
The model also assumes that volatility over a set period can be treated as constant, and in particular does not depend on the strike, which again is the reference price for the option. But if you plot volatility versus price change for historic asset price data it turns out that there is a distinct smile shape, with volatility lower for periods over which the price change is small, and climbing higher as the price change becomes increasingly positive or negative. (Note that price change is clearly related to the strike price, since options with different strikes can be viewed as the same option with a corresponding assumed price change.) A similar “volatility smile”, though somewhat less pronounced, is seen when the implied volatility used by traders is plotted versus strike – a clue left in plain sight.
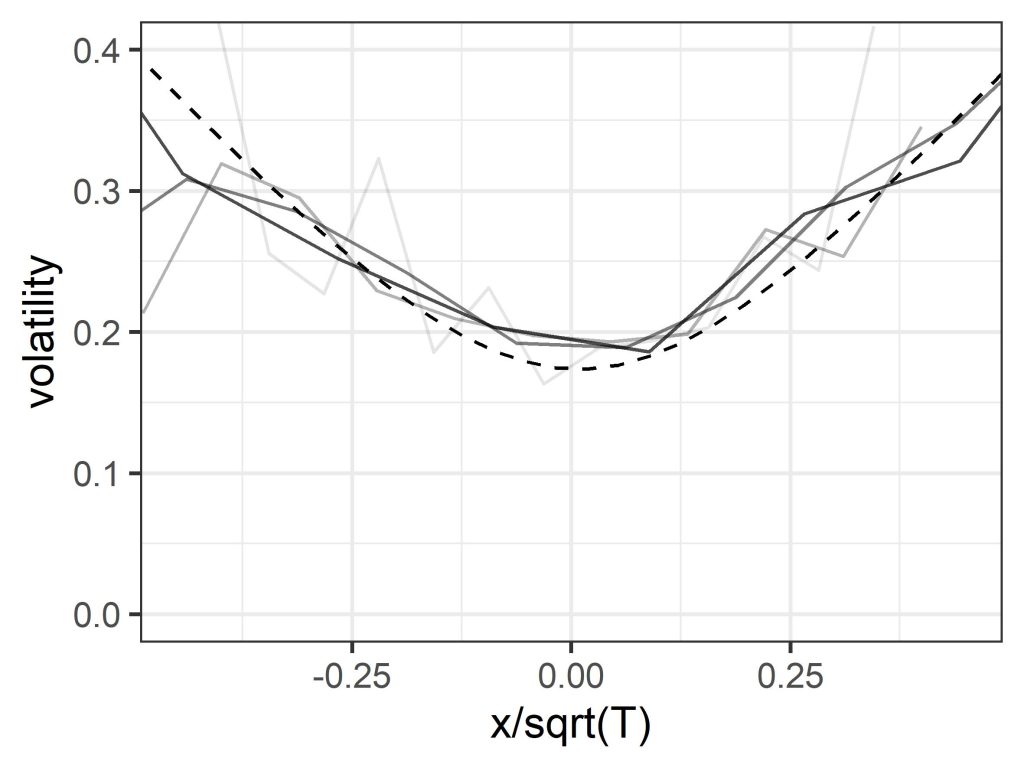
Finally, that dynamic hedging proof, which in a wave of its magic wand appeared to remove the dependence on subjective estimates of future growth, demands that you can constantly buy and sell securities and options to eliminate risk. This ignores the bid-ask spread (the difference between the buyer price and the seller price) on those transactions – which is not a technical detail, but represents a level of irreducible uncertainty, whose magnitude is related to the volatility. Include those, and the clarity, certainty, and elegance of the mathematical demonstration loses some of its theatrical sparkle. (The dashed line in the above figure was derived from a quantum economics model, which uses a different kind of magic.)
How to be beaten by the market
Now, most people in the audience will be untroubled by these details – or won’t perceive them at all – because they will tell themselves that (a) the model has a great back story and is rooted in highly rational mathematics, and (b) what ultimately counts is that the magic formula is widely known to give the “right” answers (i.e. correct predictions of the fair price), at least if we set aside the occasional stage malfunction such as the 1987 Black Monday crash, the 1998 LTCM blow-up, the 2007/8 financial crisis, and so on, where use of the model led to large losses. (Advocates of efficient market theory can explain all of these, thus falsifying the theory that theories in finance can ever be falsified.) Any nagging doubts can be addressed by inventing elaborate excuses, or by noting that no model is perfect, the Black-Scholes model has the advantage of simplicity, it is very useful as a mental tool, traders adjust the price anyway, and so on.
Only, the model doesn’t give the right answers, its predictions are off, the crystal ball is cracked. Here’s another clue: suppose you agreed to buy lots and lots of 1-month at-the-money S&P 500 straddle options (a combination of a call and a put), at the price suggested by the model using the benchmark (VIX index) volatility, and kept reinvesting the takings. If markets are efficient, and the model is telling the truth, then in principle you should expect to break even over a sufficiently long period of time. Except you won’t, you’ll lose money, in an efficient manner (this is not financial advice). In fact, you would overpay by a factor about equal to the square-root of two.
Losses will be reduced if you pay the actual market price for these options, since traders feed the oracle a lower volatility number, but they will still be significant, which again seems to contradict the efficient market hypothesis. The reason is that volatility, which is the mysterious essence at the heart of the trick, isn’t actually a thing, at least in the sense assumed by the formula. You can measure price changes over a previous period and calculate a standard deviation. Since conditions are always changing, the answer you get will depend on the exact period, so you might try to adjust for this somehow. But if the future variability is itself a highly variable quantity which depends, like expected price change, on the state of the market, then there is no single volatility that is independent of strike.
Also, since dynamic hedging isn’t a thing either, the assumption that the growth rate equals the risk-free rate – with no need for subjective estimates or uncertain predictions – is itself just a particular choice or prediction, and one which is not backed up by empirical data. The whole carefully-constructed illusion of deterministic objective rationality shatters into pieces.
All this won’t spoil the entertainment as long as people don’t look too hard behind the scenes, or check what’s going on using actual statistical tests (there being more data now than in 1973). But this still leaves the question of how this trick works. How does it get so many people to take the word of an elegant but obviously idealised mathematical proof, instead of confirming whether option prices correspond to expected payouts, which is the normal test for a statistical predictive model? Or to go along with the idea that the volatility smile is a puzzling anomaly or “logical inconsistency” (as it has been called) caused by market quirks, or irrational behaviour on the part of traders, instead of being a reflection of a real phenomenon? And how does a square-root of two error get magicked out of existence?
The logic hack
Part of the reason for the trick’s success is that, as already mentioned, it substitutes the usual test of a model, which is to predict outcomes, with a different test, which is to obey an abstract proof based on certain assumptions, thus again rendering it unfalsifiable. But at a deeper level, the secret behind the trick is that it induces in its audience what might be described as model blindness. As quants Emanuel Derman and Michael Miller (2016) note, the model “sounds so rational, and has such a strong grip on everyone’s imagination, that even people who don’t believe in its assumptions nevertheless use it to quote prices at which they are willing to trade.” By hacking (like a hypnotist on a hapless showgoer) into people’s ideas about rationality, it changes their perception of reality, and even the language they use to describe it, so the model’s word takes precedence over observable facts (the smirking volatility, the money-losing options). Which is quite a mind-blowing stunt.
Of course, like most tricks it wouldn’t have worked if the people in the gallery hadn’t at some level wanted it to work. But the real audience back in the 1970s, when it first came out, wasn’t just options traders – it was society as a whole. The illusion of predictability, objectivity and rationality was at the time in a sense necessary and productive, because it transformed options trading from a slightly disreputable form of gambling, into scientific risk management, and thus helped conjure into existence much of the quantitative finance industry. A shared language acted as a coordination device which allowed traders to communicate and do business. The audience was therefore part of the performance, and shared in the magical profits (one could even say that they, more than the inventors themselves, were the magicians who made the trick work). And it was all just one component in an even longer-running magic show, which is the neoclassical illusion that the complex, unstable, living system known as the economy is actually a rational, efficient, utility-maximising machine. Magicians have traditionally tried to convince people that the automaton is alive, but here it is the other way round.
The Black-Scholes model is one of the greatest mathemagical tricks of all time. But now, it might be time for us to snap out of this illusion, open our eyes, and let go of this idea that markets are efficient and obey rational logic. After all, it always did sound a little crazy.
An earlier version of this article appeared in the July 2023 issue of Wilmott Magazine.